PART 1 Camera Model
所謂 Camera model 是使用幾何(geometry)的方式描述真實世界中的物體在 camera 影像平面上的成像方式. 本文會說明最基本的 camera model, 也就是針孔攝像頭模型(pinhole camera model). 另外, 使用鏡片(lens)可以增加進入成像平面的單位時間光線總量,因此縮短了曝光所需要的時間, 但是使用lens也造成了影像或多或少產生了畸變(distortions), 因此我們還需要了解 lens distortion model.
有了camera 的 geometry model 以及 lens 的 distortion model 就可以建構完整的 camera 的內部參數(intrinsic parameter), camera calibration 需要使用到 camera 的內部參數.
攝像頭模型 (Camera model)
如圖一, 若是把被攝物體直接放置在成像平面之前, 被攝物體是否可以在成像平面上清晰成像呢? 答案是否定的, 因為光線是直線前進的, 光線擊中被攝物體的 A 點後, 除了一部分光線被該物體吸收, 其餘的光線將會朝向四面八方漫射, 這種狀況使得被攝物體上的 A 點無法在成像平面上形成唯一的對應光點, 同理, 被攝物體上的其他點也都無法產生清晰的影像. 因此, 這樣的置放方式, 在成像平面上, 將只會有一片模糊的影像.
 |
| 圖一 |
 |
| 圖二 |
接下來, 我們根據圖二 , 建立一個 pinhole camera model.
如圖三,
 |
| 圖三 |
 |
| EQ1 |
提供另一種思考 pinhole model 的方式, 如圖四所示:
 |
| 圖四 Engraving by Albrecht Durer, 1525 |
 |
| 圖五 |
和圖三的 camera model不同的是成像平面移到了眼睛前方, 而且成像平面上的影像也不會上下顛倒. 圖五的 camera model, 由相似三角形可以得到下面的結果:
 |
| EQ2 |
整理前面的結論, 一個空間中的點 Q (X,Y,Z), 成像在二維平面的座標是 q(x,y,f), 則
 |
| EQ3 |
 |
| EQ4 |
此處 f 的單位是 mm, Sx, Sy 的單位是 pixel/mm, 整理後得公式如下:
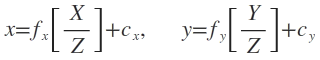 |
| EQ5 |
 |
| EQ6 |
 |
| EQ7 |
結論
本文使用簡單的方式描述成像原理, 也說明了如何建構 camera model.
fx,fy,Cx,Cy 四個參數稱為 camera 內部參數(camera intrinsic). 文章前面提到使用鏡片的好處, 但是鏡片會造成影像畸變, 因此需要校正程序把畸變校正回來, 校正程序需要使用到 camera 內部參數, 這在下一篇文章 : camera calibration part2 calibration 會做說明.
fx,fy,Cx,Cy 四個參數稱為 camera 內部參數(camera intrinsic). 文章前面提到使用鏡片的好處, 但是鏡片會造成影像畸變, 因此需要校正程序把畸變校正回來, 校正程序需要使用到 camera 內部參數, 這在下一篇文章 : camera calibration part2 calibration 會做說明.
好文!!!謝謝分享!
回覆刪除想請教兩個問題~
刪除1. 怎麼從EQ5導到EQ7的?
直觀地看,如果M如EQ7中所寫,那麼Q好像應該等於[X/Z Y/Z 1],不知道我是不是有哪個觀念漏掉?
2. EQ7中的w是怎麼出現的?對於成像平面的意義是什麼?
謝謝!
我之前也在這裡的推倒卡住, 後來這樣看就很好理解
刪除另 q' = z [x y 1] , q' = MQ (這就說的通了)
求得 q' 後, 在另 q = q' / z = [x y 1] 可求得 x y
如果有看過 opencv 的作法, 後面會有一個 / z 的動作
這樣一來整個系統就說的通了
如果將EQ7當作EQ5的衍生, 而不是直接的方程式推導. 則可發現EQ7不僅可求得成像平面上的平面座標, 還可求得物體與center of projection的實際距離.
刪除http://users.ece.gatech.edu/lanterma/mpg10/mpglecture04f10_3dto2dproj.pdf
回覆刪除國內實在難得見到camera calibration的文章
回覆刪除著實佩服
想請教
針孔成像模型中
針孔到成像平面的中心點距離為f
到成像平面上的其他點應該都大於f
好像幾乎所有的文獻都忽略掉了這點
不知是不是OpenCV的相機校正參數可修正此問題
還是我弄錯了
而且印象中相機的組合鏡頭並非一個焦點
而是形成locus
Success Write content success. Thanks.
回覆刪除betturkey
betpark
kralbet
canlı poker siteleri
deneme bonusu
kıbrıs bahis siteleri
canlı slot siteleri
Good content. You write beautiful things.
回覆刪除vbet
hacklink
sportsbet
korsan taksi
taksi
sportsbet
mrbahis
mrbahis
hacklink
ağrı
回覆刪除muş
mersin
afyon
uşak
4ZV1
salt likit
回覆刪除salt likit
L1KY
https://saglamproxy.com
回覆刪除metin2 proxy
proxy satın al
knight online proxy
mobil proxy satın al
2TNVD
https://saglamproxy.com
回覆刪除metin2 proxy
proxy satın al
knight online proxy
mobil proxy satın al
7TUZ2M
https://bayanlarsitesi.com/
回覆刪除Ordu
Kocaeli
Düzce
Osmaniye
03O
tekirdağ
回覆刪除tokat
elazığ
adıyaman
çankırı
5AA
ankara parça eşya taşıma
回覆刪除takipçi satın al
antalya rent a car
antalya rent a car
ankara parça eşya taşıma
FHJPSE
7517F
回覆刪除Balıkesir Parça Eşya Taşıma
Malatya Lojistik
Ordu Evden Eve Nakliyat
Kırıkkale Parça Eşya Taşıma
Ankara Lojistik
B7E76
回覆刪除Ankara Boya Ustası
Ankara Evden Eve Nakliyat
Isparta Parça Eşya Taşıma
Bingöl Evden Eve Nakliyat
Karapürçek Parke Ustası
Şırnak Şehir İçi Nakliyat
Yozgat Şehir İçi Nakliyat
Ağrı Lojistik
Gate io Güvenilir mi
6890D
回覆刪除Huobi Güvenilir mi
Bingöl Şehir İçi Nakliyat
Eskişehir Şehirler Arası Nakliyat
Giresun Lojistik
NWC Coin Hangi Borsada
Arbitrum Coin Hangi Borsada
Sincan Boya Ustası
Trabzon Şehir İçi Nakliyat
Sivas Parça Eşya Taşıma
252C3
回覆刪除Maraş Lojistik
Elazığ Şehir İçi Nakliyat
Osmaniye Şehirler Arası Nakliyat
Urfa Şehir İçi Nakliyat
Btcturk Güvenilir mi
Hamster Coin Hangi Borsada
Chat Gpt Coin Hangi Borsada
NWC Coin Hangi Borsada
Aydın Şehirler Arası Nakliyat
8948F
回覆刪除Bursa Lojistik
Erzincan Şehirler Arası Nakliyat
Adıyaman Şehirler Arası Nakliyat
Bitlis Şehirler Arası Nakliyat
Bursa Şehirler Arası Nakliyat
Yozgat Şehir İçi Nakliyat
Afyon Şehir İçi Nakliyat
Siirt Parça Eşya Taşıma
Kocaeli Şehir İçi Nakliyat
690CA
回覆刪除Zonguldak Lojistik
Düzce Parça Eşya Taşıma
Sivas Parça Eşya Taşıma
Kütahya Lojistik
Çerkezköy Oto Lastik
Bartın Şehir İçi Nakliyat
İzmir Lojistik
Balıkesir Evden Eve Nakliyat
Artvin Parça Eşya Taşıma
F58F9
回覆刪除Çankırı Evden Eve Nakliyat
Urfa Evden Eve Nakliyat
Çerkezköy Cam Balkon
Şırnak Parça Eşya Taşıma
Çerkezköy Kurtarıcı
Niğde Lojistik
Pursaklar Boya Ustası
Tekirdağ Evden Eve Nakliyat
Maraş Parça Eşya Taşıma
FFE0D
回覆刪除Çankaya Boya Ustası
Batıkent Fayans Ustası
Çerkezköy Kombi Servisi
Çankaya Parke Ustası
Bitmex Güvenilir mi
Gölbaşı Parke Ustası
Kilis Evden Eve Nakliyat
Maraş Evden Eve Nakliyat
Çerkezköy Fayans Ustası
31321
回覆刪除Coin Çıkarma Siteleri
Coin Nasıl Üretilir
Bitcoin Madenciliği Nedir
Bitcoin Madenciliği Siteleri
resimlimagnet
Binance Hangi Ülkenin
Kripto Para Kazma Siteleri
Coin Madenciliği Nedir
Binance Neden Tercih Edilir
62CF1
回覆刪除Bitcoin Madenciliği Siteleri
Binance Hesap Açma
Bitcoin Nasıl Oynanır
Bitcoin Nedir
Bitcoin Kazanma Siteleri
Coin Para Kazanma
Coin Nasıl Alınır
Bulut Madenciliği Nedir
Bulut Madenciliği Nedir
16CAC
回覆刪除amiclear
B1DA3
回覆刪除https://e-amiclear.com/
CB5EB
回覆刪除en iyi rastgele görüntülü sohbet
telefonda görüntülü sohbet
bedava sohbet siteleri
en iyi görüntülü sohbet uygulaması
artvin kızlarla rastgele sohbet
karaman en iyi ücretsiz sohbet siteleri
rize sesli mobil sohbet
ağrı görüntülü sohbet odaları
afyon bedava görüntülü sohbet sitesi
34B81
回覆刪除pudgy penguins
uniswap
quickswap
pancakeswap
dappradar
yearn finance
zkswap
DefiLlama
uwulend finance
85277
回覆刪除spookyswap
dexview
defillama
dappradar
eigenlayer
pinksale
satoshivm
dexscreener
quickswap
9482A
回覆刪除okex
cointiger
güvenilir kripto para siteleri
huobi
bitcoin giriş
probit
bitget
okex
vindax
2BFBD
回覆刪除binance referans
telegram en iyi kripto grupları
kripto ne demek
mexc
gate io
binance
rastgele canlı sohbet
kraken
en iyi kripto grupları telegram
5DD38
回覆刪除kucoin
bingx
coin nereden alınır
https://toptansatinal.com/
bitexen
okex
bitget
bitcoin nasıl üretilir
binance
9852F
回覆刪除gate io
bitcoin haram mı
btcturk
4g mobil
https://toptansatinal.com/
bitrue
paribu
sohbet canlı
coinex
B6A94
回覆刪除mobil proxy 4g
bitcoin hangi bankalarda var
kripto kanalları telegram
okex
4g mobil
bitcoin nasıl kazanılır
güvenilir kripto para siteleri
bitcoin hesabı nasıl açılır
binance
شركة تسليك مجاري بالدمام 6d2pZJgzo8
回覆刪除254C5B2B53
回覆刪除instagram takipci turk
449FFD3056
回覆刪除ucuz takipçi
Dragon City Elmas Kodu
Township Promosyon Kodu
Osm Promosyon Kodu
Erasmus Proje
Lords Mobile Promosyon Kodu
Free Fire Elmas Kodu
Online Oyunlar
Pubg New State Promosyon Kodu
FA8A1031F1
回覆刪除tiktok takipçi satın al
Lords Mobile Promosyon Kodu
Coin Kazan
Türkiye Posta Kodu
Bitcoin En Güvenilir Nereden Alınır
Erasmus Proje
Google Haritalara Adres Ekleme
Azar Elmas Kodu
Dragon City Elmas Kodu
CE0178B5A7
回覆刪除instagram türk takipçi
tiktok beğeni satın al
fake takipçi
gerçek takipçi
gerçek takipçi